Suppose x[n] is an absolutely summable discrete-time signal. Its

Suppose x[n] is an absolutely summable discrete-time signal. Its
| Suppose x[n] is an absolutely summable discrete-time signal. Its z-transform is a rational function with two poles and two zeroes. The poles are at z = ±2j. Which one of the following statements is TRUE for the signal x[n]?

A. It is a finite duration signal.

B. It is a causal signal.

C. It is a non-causal signal.

D. It is a periodic signal.

Please scroll down to see the correct answer and solution guide.

Right Answer is: C

SOLUTION

Concept:

  • If a sequence is absolutely summable, then its DTFT will exist and the ROC will include the unit circle.
  • If ROC includes the unit circle then the system will be a non-causal system, because causal systems are right-sided signals with ROC extending to the right side of z-plane.

Analysis:

  • Given sequence is summable, so its ROC will include the unit circle, which implies that the DTFT exists.
  • Poles location shown below:


     
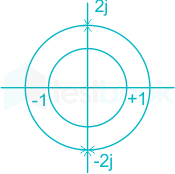
  • Here ROC includes the unit circle as can be easily seen from the above graph which means that the ROC is left sided.
  • Hence it is a non-causal system

  • So Option 3 is Correct.

Related Questions